In mathematics, a logarithm is like a superhero, swooping in to rescue us from complex multiplication and division problems. Let’s dive into the world of logarithms!
Logarithms come in two flavors:
– Common Logarithms: Base 10
Example: Log(100) = Log10(100) = 2
– Natural Logarithms: Base e
Example: Ln(25) = Loge(25) = 3.21887
Our Heroic Equation:
f(x) = logax
For our example, we’ll examine the function: f(x) = log2(x)
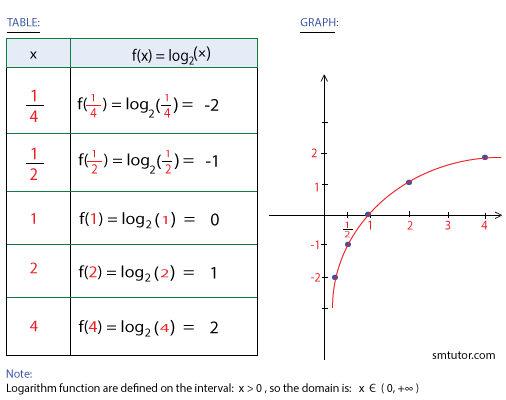
Understanding the Graph:
- Logarithmic functions are defined for x > 0 or x ∈ (0, +∞).
- You can’t evaluate log2(0)
- Logarithms of negative numbers result in an ERROR or log2(zero) = ERROR
Solving Logarithmic Expressions:
a) Examples: Let’s unravel these logarithmic mysteries:
Find for: log2(32) = ?
Solution:
The quest is to find a number where 2number = 32
b) Examples: More adventures in logarithms:
Find for: log10(10000) = ?
Solution:
Ready for more logarithmic heroics? Download our free courses and become a logarithm master! 🚀📚
