Understanding Quadratic Equations
In mathematics, quadratic equations are a fascinating branch that involves squares. The term “quadratic” is derived from the Latin word “quad” which means “square.”
Quadratic Equation Form:
ax2 + bx + c = 0
Here, a is a non-zero constant, while b and c represent known values.
Example:
Consider this quadratic function: x2 + 4x + 3
Standard Form:
ax2 + bx + c = 0
It’s crucial to note that a must not equal zero. In this equation, a, b, and c have specific values.
The degree of a quadratic equation is 2, and the unknown variable is typically represented as X.
Solving Quadratic Equations:
a) Example 1: Let’s solve the following quadratic equation using the Completing the Square method:
Completing the Square: x2 + 6x + 8 = 0
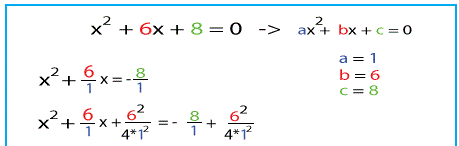
How to Solve Quadratic Equations in 3 Cases:
- Case 1: Solve by Completing the Square.
- Case 2: Solve by Factoring the Quadratic.
- Case 3: Solve using the Quadratic Formula:
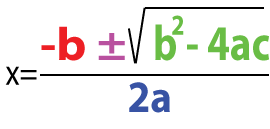
Explore more examples and download free courses:
Download the free courses
Explore more examples and download free courses:
Download the free courses
In conclusion, quadratic equations are a fundamental concept in mathematics, rooted in the idea of squares. They are represented by the standard form ax2 + bx + c = 0, where a is nonzero. Solving quadratic equations involves various methods such as Completing the Square, Factoring, and using the Quadratic Formula. Continue exploring and practicing to master this essential mathematical skill.
