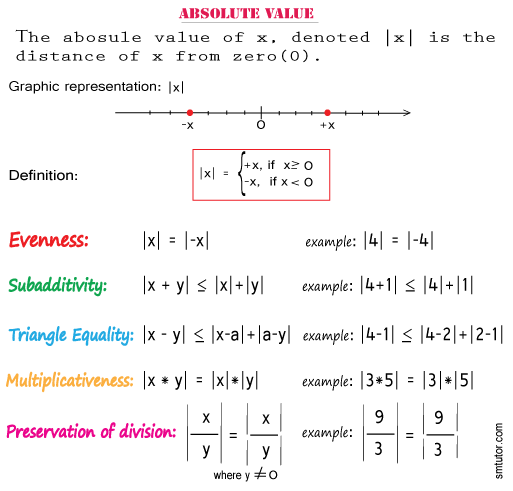
Note that there are two approaches to defining absolute value. The first approach is through a geometrical concept, while the second approach is the mathematical definition.
- Absolute value of x is noted: | X |
HOW TO SOLVE ABSOLUTE VALUE EQUATIONS
 |
Cases1. Solving by Mathematical definition.
Cases2. Solving by Graphical Definition.
a) Example 1: Solve the following absolute value equation.
Solve: | x | = 6
Solution:
To solve absolute value equations, we need to separate the absolute value into two parts: The first part is the (+) positive side, and the right side is the (-) negative side. See below:

Solve: | x + 4 | = 6
b) Example 2: Solve the following absolute value equation.
Solution: Download the free courses
Understanding absolute value equations is essential in mathematics. By mastering the methods to solve these equations, you can handle a wide range of mathematical problems that involve absolute values.
Download the result Above
Remember, absolute value equations are fundamental in various mathematical applications, from solving real-world problems to advanced calculus and algebra. Continue to explore and practice these concepts to enhance your mathematical skills.
