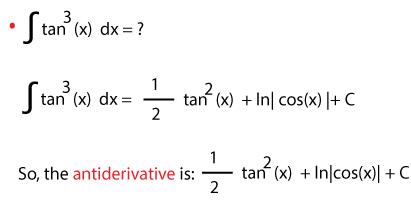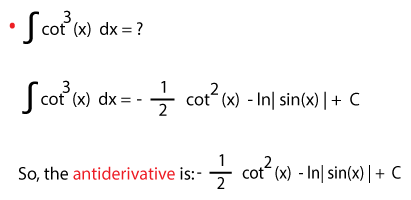HISTORY
Derivation is very important in mathematics, especially in calculus.
Appeared by the end of the 16th century, this concept was developed during the 17th century, by a great German philosopher and scientist named Gottfried Wilhelm Leibniz (1646-1716) and also by a great English scientist and inventor named Sir Isaac Newton(1642-1727).
Leibniz N0tation:
Note the German scientist Gottfried Wilhem Leibniz (1646-1716)introduce the following notation: df/dx .
Note the French mathematician Joseph Louis Lagrange (1736-1813) introduce the “prime” notation f ‘(x).
TRIGONOMETRY ANTIDERIVATIVES:
List of some mathematic formulas here: Derivative, Integral, and more…
EXAMPLE 1:
| Find the anti-derivative of f(x) = ∫[tan3(x)]dx
Solution:
|
EXAMPLE 2:
| Let us find the anti-derivative of f(x) = cot3(x)Solution:
|