Note that there are two (2) approaches in defining absolute value. The first approach will determine the absolute value through a Geometrical concept. The second approach will be the mathematic definition.
- Absolute Value Inequality: Example: | X | ≥ 0 or | X | ≤ 0
See below for an explanation:
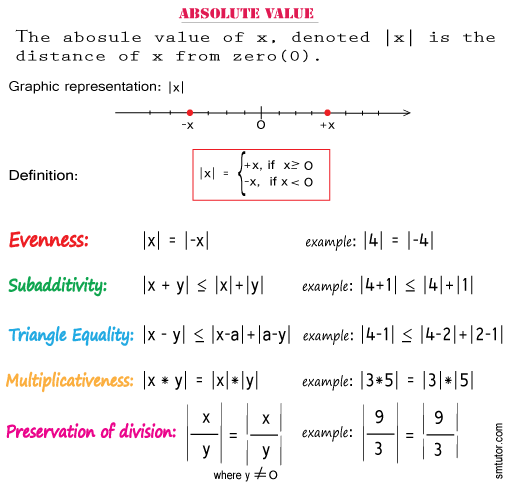 |
HOW TO SOLVE ABSOLUTE VALUE INEQUALITY.
- Cases1. Solving by Mathematical definition.
- Cases2. Solving by Graphical Definition.
a) Example 1: Solve the following absolute value Inequality.
Solve: | x + 3 | < 5
Solution:
Note, to solve absolute value Inequalities we need to follow the rule of “LESS THAN”
So, If absolute value of x noted | x | < b therefore the solution is: – b < x < b
Solve: | x – 4 | > -3
a) Example 2: Solve the following absolute value Inequality.
Solution: Download the free courses
